BTC比特币为什么是2100万枚?为什么比特币只有2140万枚?比特币为什么最多2100万?虽然网上有很多关于解说比特币只有2100万枚的事情,但是看完这篇文章,感觉认知更加清晰!
Why is it 21 million? Why is it only 21.4 million? Why is it 21 million? Why is it 21 million?

一片花飞减却春,风飘万点正愁人;
The flowers are falling and the wind is a little sad.
且看欲尽花经眼,莫厌伤多酒入唇。
And look at the eyes, and do not be tired of hurting the lips with a lot of wine.
五月的加密市场,BTC(比特币)在6万刀踟蹰不前,春去花落一片红。无甚热闹,但徜徉湖边,看绿水青山,心底宁静,仓位致远。
In May, the encryption market, BTC (bitcoin) fell red in the spring at 60,000 blades. There was no fun, but on the edge of the lake, looking at the green mountains, calm and far away.
BTC乃加密行业之根。总量2100万之上限,乃BTC之本。一切都从这个神奇的数字展开。可是它,为何是这样一个数字呢?
The BTC is the root of the encryption industry. The upper limit of 21 million is the BTC. Everything goes from this magic number. But why is it such a number?
教链在2020年12月5日文章《为什么比特币最多只会有2100万枚?》中,就曾介绍过这个数字的计算方法。简而言之是这样的:
In a December 5th, 2020 article, " Why does Bitcoin have a maximum of 21 million? ", a calculation of this figure was presented. In short:

1. 每区块产量 50 BTC
1. Production per block 50 BTC
2. 每21万个区块,产量减半
2. Halve production per 210,000 blocks
使用等比数列求和可以轻松算出,最终BTC的总产量为:(50 + 25 + 12.5 + 6.25 + 3.125 + ...) x 21万=2100万枚。
It is easy to calculate using the equation column, and the total production of BTC is: (50 + 25 + 12.5 + 6.25 + 3.125 +...) x 210,000 = 21 million.
进一步的,调节“挖矿”难度使得大约每10分钟产生一个新区块,即每小时6个新区块,21万个区块就大概是人间4年。
Further, regulation & ldquo; mining & rdquo; difficulty makes it possible to produce a new block approximately every 10 minutes, i.e. 6 new blocks per hour, or 210,000 blocks for approximately four years.
这也就是比特币4年产量减半周期的来历。
This is the history of the four-year cycle of halving the production of Bitcoin.
但是,如此只是对既定事实的一个铺叙而已。一是缺乏一些细节的考察;二是并未真正揭示比特币发明人中本聪为何要选择和设计这样一个数字的原因。
But this is only a description of the established facts. First, there is a lack of detail; and second, there is a lack of real clarity as to why a bitcoin inventor should choose and design such a number.

首先,
First of all,
2100万并非2100万,而是2,099,999,997,690,000。对,后面这个数字比2100万要大1亿倍,即大约是2100万亿。在比特币系统内部,都是这个万亿级的整数。
21 million is not 21 million, but 2,099,999,997,690,000. Yes, that figure is 100 million times larger than 21 million, or about 21 trillion. Within the Bitcoin system, it's a trillion-dollar whole.
当我们把BTC“展示”为这个整数点上8位小数位,也就变成了2 0,99 9,99 9.97 690 000。这里我用空格提示了上面作为整数时的千分位分割点。我们一眼就会看到,中本聪选择8位小数位其实有些奇怪的,因为这样会导致8位小数的BTC整数部分的逗号分割点,和系统内真正的整数的逗号分割点不一致。
When we take BTC“ show & rdquo; for this integer point, eight decimal places become 20,999,997,690,000. Here I use the space to hint at the point of the thousands of fractions of the integer. As we can see at first glance, the choice of the eight decimal places by the mid-digit is somewhat strange, because it would result in a comma split of the eight decimal parts of the BTC, which would be inconsistent with the actual commas of the whole number of the system.
8位小数位,也就是1亿分之一,这个就不太西方。众所周知,英文里对数字采用千分位分割,所以计数法的单位是千(thousand)、百万(million)、十亿(billion)、万亿(trillion)。英文里并没有“亿”这个单位。而中国的计数法略有不同,是以4位数字也就是万分位为分割的,乃有万、亿、万亿。
Eight decimal places, one in 100 million, are less Western. As you know, the figures are divided by thousands in English, so the numbers are in thousands, millions, billion, trillion, trillion. There is no “ billion & rdquo; this unit in English.
2100万亿用万分位分割就是这样的:2099 9999 9769 0000;2100万带8位小数则是这样的:2099 9999.9769 0000。都是4小节,每小节4位数字,没有任何混乱。所以看起来,8位小数位,1亿分之一,嗯,这很东方。
This is the case with 21 trillion billions divided in thousands: 2099 9999 9769000; 21 million with eight decimal places: 2099 9999.9769000. It's four subsections, four digits per subsection, no confusion. So it looks like eight decimal places, one in 100 million, and, uh, it's Eastern.
其次,
Second,
2100万亿之所以是2,099,999,997,690,000而不是精确的2,100,000,000,000,000,也正是因为8位小数位的精度限制。
The 21 trillion is the 2,099,999,997,690,000 instead of the precise 2,100,000,000,000,000,000, and is precisely due to the eight-digit precision limit.
上文的等比数列(50 + 25 + 12.5 + 6.25 + 3.125 + ...)并非真正的无穷数列,而是当它减小到0.0000 0001之后,再减半就归零了。因此,这是一个截断了的有穷数列,其加和就要小于无穷数列求和的结果100。所以,乘以21万之后,最终结果也要略小于2100万。
The equivalency column above (50 + 25 + 12.5 + 6.25 + 3.125 + ) is not really an infinity, but it is reduced by half to zero when it is reduced to 0.000 0001. So, it is a cut-off number, plus less than a hundred. So, multiplied by 210,000, the end result is slightly less than 21 million.
第三,
注意第一点的叙述,8位小数位和小数点仅仅是一个“展示”层面的设计。在系统内部只有那个万亿级的整数。
Take note of the first point, eight decimal places and decimal points are just one & ldquao; display & & rdquao; layers of design. There's only one trillion integer in the system.
既然仅仅是“展示”,那么其实小数点是可以任意挪动的。现在点在8位小数的位置,以后也可以点在5位或者4位小数的位置。
If it's just & & ldquao; display & & rdquao; then the decimal points can be moved at will. Now it's in eight decimal places, then it's in five or four decimal places.
比如,20,999,999,976.90000(5位小数),或者2099 9999 9769.0000(4位小数)。
For example, 20,999,999,976,900 (five decimal places) or 2099,999,97690.000 (four decimal places).
那么,8位小数时的1枚比特币,当移位到5位小数时,就显示为1000,移位到4位小数时,就显示为10000。相应的,原来的0.001或者0.0001 BTC现在就会显示为1。
So, one bitcoin at eight decimals shows 1000 when moving to five decimal places and 10,000 when moving to four decimal places. Correspondingly, the original 0.001 or 0.0001 BTC is now shown to be 1.
这移位的想法并非教链杜撰的,而是中本聪真实的想法。在2009年4月12日中本聪给Mike Hearn的回信[1]中,他这样写道:
The idea of a transfer is not made up by the church chain, but by the heart of the truth. in his reply to Mike Hearn on 12 April 2009, he wrote:
原文:
Original:
"My choice for the number of coins and distribution schedule was an educated guess. It was a difficult choice, because once the network is going it's locked in and we're stuck with it. I wanted to pick something that would make prices similar to existing currencies, but without knowing the future, that's very hard. I ended up picking something in the middle. If Bitcoin remains a small niche, it'll be worth less per unit than existing currencies. If you imagine it being used for some fraction of world commerce, then there's only going to be 21 million coins for the whole world, so it would be worth much more per unit. Values are 64-bit integers with 8 decimal places, so 1 coin is represented internally as 100000000. There's plenty of granularity if typical prices become small. For example, if 0.001 is worth 1 Euro, then it might be easier to change where the decimal point is displayed, so if you had 1 Bitcoin it's now displayed as 1000, and 0.001 is displayed as 1."
翻译:
“我对硬币数量和发行时间表的选择是经过深思熟虑的。这是一个艰难的选择,因为一旦网络开始运行,它就会被锁定,我们就会被它困住。我想选择一种能让价格与现有货币相近的(数字),但在不知道未来的情况下,这很难做到。最后,我选择了中间值。如果比特币仍然是一种小众货币,那么它的单位价值就会低于现有货币。如果你想象比特币被用于世界商业的某个部分,那么全世界只有 2100 万个比特币,所以它的单位价值会更高。币值是小数点后 8 位的 64 位整数,因此 1 枚硬币在内部表示为 100000000。如果典型(应用场景的)价格变小,则有足够的粒度。例如,如果 0.001 价值 1 欧元,那么改变小数点的显示位置可能会更容易(查看和使用),所以如果你有 1 个比特币,现在显示为 1000,而 0.001 显示为 1。”
& & ldquo; My choice of coin numbers and distribution schedules is well thought out. This is a difficult choice, because once the network starts operating, it will be locked, and we will be trapped in it. I want to select a number that will bring prices close to the current currency, but it will be difficult to do so without knowing the future. Finally, I chose the middle value. If Bitcoins are still a small currency, then their unit value is lower than the current currency. If you imagine that bitcoins are used in some part of world commerce, there are only 21 million bits in the world, so its unit value is higher. If you have eight bits after the decimal, then one coin is worth 64 integer, and it is 100000 in the interior. If the typical (applicative scenario) prices are smaller, there are enough particles. For example, if Euro001 is worth, it may be easier to change the location of the decimal points (see and use), so if you have 1 particular currency, it is now shown at 1000; & qu;
有人说,对于普遍的64位计算机而言,如果我们使用64位二进制数同时表示整数和小数(又称浮点数),那么最安全的做法是把整数限制在浮点数的整数部分可表达的上限内。
It has been said that, for 64 computers in general, if we use 64-digit binary numbers to indicate both integer and decimal numbers (also known as floating points), the safest way is to limit the integer to a maximum that can be expressed in the integer part of the floating point.
稍微了解计算机原理的朋友都知道,计算机内部并没有什么小数,都是0和1的数位。所谓64位整数,就是指64个0或者1所组成的二进制整数。对应10进制就是2^64=18446744073709551616。这个数字要远大于2100万亿。但是,如果要让计算机能够处理浮点数,那么就要把64位中拆出一部分用来表达小数部分,还要留出1位来表示正负号。这就成了IEEE 754浮点数编码标准。其中标准定义,双精度浮点数用64位二进制是这样编码的:
A friend who knows a little bit about computer principles knows that there are no decimals in the computer, either 0 or 1 digits. The 64-digit integer is a binary integer of 64 zeros or 1s. The corresponding 10-digit is 2⁄64 = 1844447473709551616. This figure is much greater than 21 trillion. But if the computer is to be able to process floating points, then a portion of the 64-digit is to be removed to express decimals and one to indicate positive or negative numbers. This is the IEEE 754 floating point coding standard.
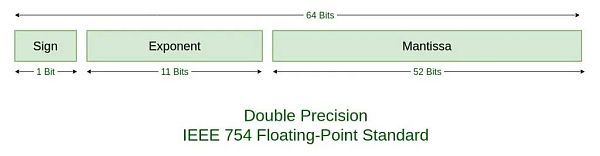
这样一来,整数部分就只能使用53位,也就是最大不超过2^53=9007199254740992。而如果希望容易测试结果是否为整数,则最好不要超过2^51=2251799813685248。如此,可以选择22(百万亿),但是22不是一个“三角数”(triangular number),所以中本聪选择了21(百万亿)。
In this way, the whole part can be used only 53 places, i.e. a maximum of 2⁄53 = 9007199254040992. And if it is hoped that the results will be easy to test, it is better not to exceed 251 = 225179981365248. Thus, 22 (millions) can be chosen, but 22 is not “ ” triangular number, so Middle-Hear chose 21 (millions).

据此许多人认为中本聪选择2100万亿,大大地方便了各种编程语言处理比特币数量相关的计算。
As a result, many people believe that the choice of 21 trillion dollars for China has greatly facilitated the processing of Bitcoins-related calculations in various programming languages.
不过,教链看了中本聪的邮件后,觉得中本聪也许并没有这么复杂的想法。或者他的确思忖过,但是并没有讲透他的全盘考虑。他只是讲,也曾经考虑过其他数字,比如4200万亿,但是感觉太大了,于是就折中成了2100万亿。在2011年1月10日中本聪回复Mike Hearn的邮件[2]中,他是这样写的:
However, after looking at the medium-breathing e-mail, the chain felt that it might not be that complicated. Or he thought about it, but he didn't think about it as a whole. He simply said that he had considered other figures, such as 42 trillion, but it felt too big, and it was 21 billion. In his reply to Mike Hearn’s e-mail on January 10, 2011, he wrote:
"It works out to an even 10 minutes per block:
21000000 / (50 BTC * 24hrs * 365days * 4years * 2)=5.99 blocks/hour
"I fudged it to 364.58333 days/year. The halving of 50 BTC to 25 BTC is after 210000 blocks or around 3.9954 years, which is approximate anyway based on the retargeting mechanism's best effort.
"I thought about 100 BTC and 42 million, but 42 million seemed high.
"I wanted typical amounts to be in a familiar range. If you're tossing around 100000 units, it doesn't feel scarce. The brain is better able to work with numbers from 0.01 to 1000.
"If it gets really big, the decimal can move two places and cents become the new coins."
看起来,中本聪是先定了时间诸参数,而后调整区块产量和总量,并思考多大的数字较为适合。
It appears that China has set time parameters before adjusting the output and volume of blocks and considering what numbers are more appropriate.
依中本聪的意思,大多数人手里的BTC数量最好在0.01到1000之间,不要动辄就搞个6、7位数的币,那样会缺乏稀缺感。
In the middle sense, most people have between 0.01 and 1,000 BTC in their hands, and there's no sense of scarcity in getting six or seven digits.
比特币总量2100万个,这可能是刚接触比特币的小白们记得最清楚,也是最迷惑的数字。中本聪没在任何公开的言论中提到:为什么选这个数字,于是网上出现了各种各样的猜测和逻辑推理。
A total of 21 million bitcoins, probably the whites who have just touched bitcoin, remember the most, and the most confusing, figure. Benz did not mention in any public statement why this number was chosen, and there was a variety of speculations and logical reasoning on the Internet.
【1】20999999.97690000
最终产生的比特币数量,准确的说是20999999.97690000个,比2100万少一点。
The resulting number of bitcoins, to be exact, is 209999999.9769 thousand, a little less than 21 million.
比特币产生的时间表:
Timelines generated by bitcoin:
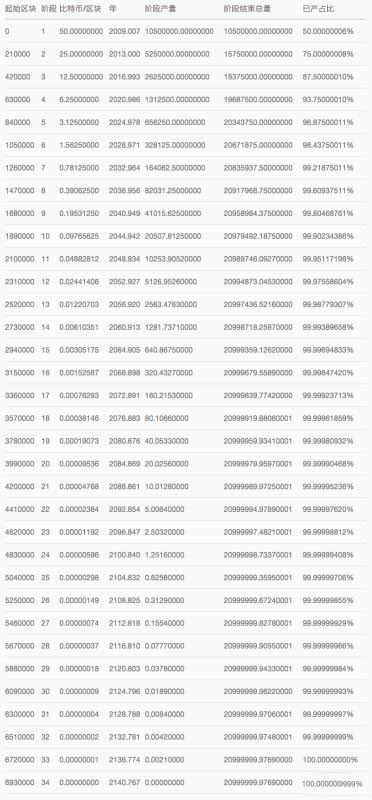
下面挑几个重点分析一下这张表。
Here's a few highlights to analyse this table.
【2】50.00000000
格林威治时间2009年1月3日18:15:05,创世区块诞生。创世区块的编号是0。从创世区块开始的”阶段1”,每个区块产生50个新的比特币或者说50亿聪。
Greenwich time, 3 January 2009, at 18:1505, the Genesis Block was born. The number of the Genesis Block is zero. The & rdquao; Phase 1 & rdquao; each block produces 50 new bitcoins or 5 billion words.
创世区块:https://blockchain.info/block-height/0
【3】目标高度210000
格林威治时间2012年11月28日15:24:38,编号第210000个区块产生。从这个区块起的”阶段2”,每个区块包含的新比特币数量减半为25个,这是历史上第一次减半。今后每产生210000个区块,比特币数量都会依次减半。直到第33次减半时,每个块产生0.0021个新比特币直接减为0个。
Greenwich Time, 28 November 2012, 15:24:38, No. 210,000 blocks. From this block, ” phase 2&rdquao; and, for the first time in history, the number of new bitcoins per block is reduced by 25 by half. For every 210,000 blocks, the number of bitcoins will be reduced by half. Until the 33rd time, the number of new bitcoins per block will be reduced directly to zero.
210000块:https://blockchain.info/block-height/210000
【4】4年1次的约定
每4年减半是不太严格的说法。实际情况:比特币大约每10分钟产生一个区块,而210000个10分钟接近4年(4年等于210384个10分钟。这应该是中本聪特意选取的数字)。
Halve it every four years is not a very strict term. In reality: Bitcoin produces about one block every 10 minutes, while 210,000 10 minutes are close to 4 years (four years equals 210884 minutes). This should be the figure that should have been chosen by China.
【5】2016前,2016后
[5] by 2016, after 2016
2016年将发生第二次减半,但现在讨论这个有点早。我要说的是2016个块的问题。
There will be a second reduction by half in 2016, but it's a little early to discuss. I'm talking about the 2016 block.
比特币系统调节挖矿难度的原理是:根据前2016个块产生的总时间,调整后2016个块的挖矿难度,让挖出这2016个块的时间为14天。因为,每小时6个10分钟乘以24小时再乘以14天=2016。所以,所谓10分钟只是平均值目标。由于目前算力上涨很快,实际上挖出2016个块的速度往往少于14天。
The rationale behind the Bitcoin system to regulate the difficulty of mining is that, based on the total time generated by the first 2016 blocks, the difficulty of mining the next 2016 blocks is adjusted to allow for the recovery of the 2016 blocks to take 14 days. Because, 6 minutes per hour multiplied by 24 hours multiplied by 14 days = 2016. So the 10 minutes are the average target. Because of the current rapid increase in computing power, the rate of excavating the 2016 blocks is often less than 14 days.
难度调整的话题涉及到挖矿,以后再一并分析。
The topic of difficulty adjustment relates to mining, which will be analysed at a later stage.

网络上有很多种猜测,有些很靠谱,有些不靠谱但很欢乐。
There are a lot of speculations on the Internet, some sound and some unsound but happy.
【答案1】
It's the first half of the answer: 42.
翻译:因为21是终极答案42的一半。
Translation: Because 21 is half of the final answer to 42.
(说明:英语里,2100万表示为:21 million。所以,老外一般直接问:为啥是21。)
(Note: In English, 21 million means 21 million. So, foreigners usually ask directly: Why 21?
当然,他是开玩笑的。不过,我个人最喜欢这个猜测,这也是reddit里顶的人最多的。
Of course, he's joking. But, personally, I love that guess, and it's the highest number of people in Reddit.
这个梗来自电影《银河系漫游指南》里终极答案的桥段。
This is the bridge from the ultimate answer in the movie "Galactic Walking Guide".
直接看视频吧(找了一圈,只有youtube上有剪辑,所以俺加了字幕搞过来):
Just look at the video.
【答案2】
Because we re living in the 21st century!
翻译:因为我们生活在21世纪!
Translation: Because we live in the 21st century!
太天真,不忍吐槽。
That's naive. I can't stand it.
【答案3】
He chose a reward scheme and 10 minute blocks. When he did the math, it came to 21 million. He didn t choose the 21 million, he just accepted the consequence of the parameters he chose.
翻译:中本聪订好10分钟、50币、4年减半的原则,结果自然出来了。他没有选,而是接受了这个自然的结果。
Translator: The ten-minute, 50-dollar, four-year-a-half rule, naturally. He didn't choose, but accepted the natural result.
这个答案也是有可能的。中本聪在比特币中的很多选择确实是撞大运的,但都是“基于经验的撞大运”。
And the answer is also possible. Many of the choices in Bitcoin are indeed & & & & & & & & & & & & & & & & & & & & & & &.
【答案4】
All gold mined in human history can be fit into a cube roughly 21 meters on each side.
Satoshi created bitcoin with the idea of being sort of a digital analog of gold (finite supply, mining, etc), as well as the fact that it built upon Nick Szabo s “Bit Gold” proposal, so I think that 21 million was sort of a clever nod to that.
翻译:全世界所有黄金熔在一起,是一个边长大约为21米的正方体。中本聪用这个概念,隐喻比特币是一种虚拟黄金。
Translation: All the gold in the world melts together as a square, growing about 21 metres apart. In this concept, the metaphoric bitcoin is virtual gold.
原来阴谋论不止中国有
So there's more to conspiracy theory than China.
【答案5】
I was going to say: Satoshi likes to play Vegas blackjack.
翻译:我觉得中本聪喜欢玩21点。
Translator: I think Nakamoto likes to play at 21 o'clock.
上帝玩骰子么?
Does God play dice?
【答案6】
计算机双精度浮点数最多存储2^53精度的数。而比特币按最小单位算的总精度是2^51,刚好够用。(英文太长不贴了)
The computer's double-precision floats hold up to a maximum of 2:53 accuracy. The total accuracy of bitcoins in the smallest units is 2:51, which is just enough.
这个答案,出现在一篇很不错的文章里《中本聪的天才:比特币以意想不到的方式躲开了一些密码学子弹》
This answer appears in a very good article, The Talent of Mid-Sight: Bitcoin avoids some cryptographic bullets in an unexpected way.
详细:
Details:
比特币有争议的属性之一就是它的固定的供应量。当前每10分钟又25个新的比特币被生产出来,并且这一数字每4年减半。总的来讲,不会有超过2100万个比特币的存在>。另一方面,每个比特币可以被划分成1亿份(每份叫做1“聪”),如果一美分都足够买辆车的话,用美元来交易就麻烦重重了,但比特币就算升值到和上面假设的美元的>状况,也不会遇到那样的问题。
One of the controversial properties of Bitcoins is its fixed supply. Twenty-five new bitcoins are now produced every 10 minutes, and that number is reduced by half every four years. Overall, there will be no more than 21 million bitcoins > on the other hand, each bitcoins can be divided into 100 million pieces (1“ hearing & rdquo;) if a penny is enough to buy a car, the dollar will be a lot of trouble, but even if bitcoins rise to the assumed dollar & gt; the situation will not be the same.
因此,总之,将永远存在的货币单位的总数字是2,100,000,000,000,000,也就是2100万亿,或者说250.899。在选择这个数值的方>面,中本聪比大多数人意识到的要幸运的多或者说聪明的多。首先,这个数字远小于264-1,这是一台计算机里面可以以标准整数形式存放的最大整数,超过那个值的话,>数值将像里程表那样归零。
So, in sum, the total number of currency units that will remain in place forever is 2,100,000,000,000, or 21 trillion billion, or 250.899. In choosing this value > on the face of it, Ben is much more fortunate or smarter than most people are aware of. First, the figure is much smaller than 264-1, the largest integer in a computer that can be stored in a standard integer form, > the value will be zero, as in the mile scale.
其次,然而,还有一个总“聪”数要设法低于的更小的阈值:可以用浮点的格式表示的可能的最大整数。整数不是计算机可以存储的唯一一种数字;为了处理小数,计算机>使用一种做浮点表示法的格式。浮点表示法本质上就是一个科学记数法的二进制版本。举个例子,下面是一个在你学习物理学的时候会遇到的值:
Second, however, there is a smaller threshold that the total & ldquo; the deaf & rdquo; the number is managed to fall below: the possible maximum integer that can be expressed in floating point format. The integer is not the only number that a computer can store; the computer >, to process decimals, uses a floating point expression format. The floating point expression is essentially a binary version of a scientific numeric method. For example, the following is the value that you will encounter when you learn physics:
地球的质量: 5.972 1024 kg
Quality of Earth: 5.972 1024 kg
太阳的质量: 1.989 1030 kg
Solar mass: 1.989 1030 kg
光速: 2.998 108 m/s
Light speed: 2.998 108 m/s
一光年: 9.460 1015 m
One light year: 9.460 1015 m
质子的质量: 1.672 10-27 kg
Quality of protons: 1.672 10-27 kg
普朗克长度: 1.616 10-35 m
Length of Planck: 1.616 10-35 m
我们可以注意到,科学记数法是如何使得你可以在合理的精度下表示所有的这些数值,尽管它们的大小相差极大。浮点表示法本质上就是二进制的科学记数法;当你存储数>字9.625的时候,你的计算机存放的是“1.001101 * 1011”(或者说,它存放的是01000000 00100011 01000000 00000000 00000000 00000000 >00000000 00000000,这是高精度序列形式的同样一回事)。在这个高精度形式中,系数(也就是不是指数的那部分)有52位(52bits)。这意味着高精度(更加精>确的说法是“双精度”)浮点数足以存贮高达253的数字,但不能再高了,如果超过了,你就得开始砍掉末尾的数字。比特币的250.9这一以指数形式表现的总“聪”数,刚>好低于这个最大值。
We can note how scientific memory allows you to express all these values with reasonable accuracy, even if their size varies considerably. The floating point means essentially the binary scientific count; when you store > word 9,625, your computer is stored in “ +1001101 * 1011 & rdquo; or it is stored in & & & ldquo; & & & & rdquo; or it is kept in 010000 000 001001 0.000 000 & & gt; £100 million; this is the same thing in the form of a high precision sequence. In this high-precision form, the coefficient (that is not the part of the index) has 52 places (52 bits). This means high accuracy (more & gt; truely & & ldquo; double accuracy & rdquo;) the floating point is sufficient to store up to 253, but it is no longer high, and if it is exceeded, you have to cut the figure at the end.
如果我们有了整数,我们为什么还要关心浮点值呢?因为更多的高阶编程语言(比如说Javascript)并不开放低阶的“浮点”和“整数表示法”,而只给程序员提供“数”的>概念 当然以浮点的形式提供。如果中本聪当时选择了2亿1千万而不是2100万这个值的话,用很多语言里比特币编程就会比现在要麻烦得多了。
If we have the whole number, why do we care about floating point values? Because more high-level programming languages (e.g. Javascript) do not open up lower & & & & & & & & & & & ; & & & & & & ; integer expressions & & & & & & & & & & & & & & & ; concepts in the form of floating point, of course.
注意,Stefan Thomas不幸的在他写BitcoinJS的时候没有及时留意到这个,以至于那个库使用了一个专门的“大数big number”对象,而不是一个普通数来存储教程输出值;我自己分叉的的BitcoinJS(同时还加入了其他的改进)使用了普通数。
Note that Stefan Thomas unfortunately did not notice this in time when he wrote BitcoinJS, to the extent that the library used a special & ldquao; a large number of big numbers & rdquao; objects, rather than an ordinary number, to store the output value of the curriculum; and my own split BitcoinJS (with other improvements added) used a normal number.
【答案7】
That explanation is close but not entirely compelling. IEEE double-precision floating-point format has 53 bits of significand precision, meaning it can address up to 253 1 satoshis without any rounding error. Well, that s 9,007,199,254,740,991 satoshis, which is not anywhere close to 2,100,000,000,000,000 satoshis (or even 2,099,999,997,690,000 satoshis, which is the actual asymptotic limit).
I think a much more compelling explanation is that a signed 32-bit integer can store values up to 231 1, which is 2,147,483,647. If you assume a fixed-point format with two decimal digits of fractional precision (which is typical for money), then a signed 32-bit integer can address up to 21,474,836.47 bitcoins, which we might as well round off to 21 million. My guess is that Satoshi derived the 21-million limit from here early in development and then later realized that this wouldn t be enough currency units and so extended the number of decimal places from 2 to 8 and changed the variables from 32-bit to 64-bit.
翻译:答案6的解释很接近,但有点牵强。IEEE双精度浮点数是53bits,能表示的最大数是9,007,199,254,740,991聪,而比特币是2,099,999,997,690,000聪,差别还是很大的。
Translation: The explanation for answer 6 is very close, but it's a bit far-fetched. The IEEE double-precision floats are 53 bits, the largest number being 9,007,199,254,740,991 ears, while the Bitcoin is 2,099,997,690,000 ears, which is still very different.
我觉得更好的解释:有符号32位整数可存储最大2^32-1的数,是2,147,483,647。如果比特币是小数点后两位的话,就是21,474,836.47个比特币。也就是21-million。我猜中本聪在最初开发的时候用32位精度的整数,后来发现对于一种全球通用货币来说这个精度不够,所以把小数点后2位延展成8位,从32位存储改成64位存储。
I think there is a better explanation: there is a 32-digit integer to store a maximum of 2,147,483,647. If Bitcoin is the second two decimal places, it is 21,474,836.47 bitcoins. That is, 21-millition. I guess Ben was able to use a 32-digit integer when he was first developed, and later found to be insufficient for a global universal currency, so extend the 2-digit integer to 8 places, from 32 to 64-digit storage.
这是我觉得最靠谱的答案,因为从中本聪的过往言论可以看出,他不是一个完美主义者,而是一个实用主义者。
That is what I think is the most solid answer, because, as can be seen from the past, he is not a perfectionist, but a utilitarian.
研究比特币技术原理,是深入了解比特币的最佳途径,也是推动比特币行业发展的基石。希望国内有更多专业的开发、技术专家进入这个领域。还有,炒币虽爽,盯盘伤身,切记切记!
Research on bitcoin technology is the best way to gain insight into bitcoin and the cornerstone of the development of the bitcoin industry. It is hoped that there will be more professional development and technocrats in the country. And, while they're cool, they're hard to look at, remember!
以上就是脚本之家小编给大家分享的BTC比特币为什么是2100万枚?BTC比特币2100万枚的由来介绍了,看完此篇文章大家对比特币的由来了解的更加简单!
That's why the BTC bitcoin shared with you at the Script House is 21 million? The BTC bitcoins of 21 million were introduced.
注册有任何问题请添加 微信:MVIP619 拉你进入群

打开微信扫一扫
添加客服
进入交流群

















发表评论